 |
Robust causal inference using non-randomized longitudinal data |
Philip Clare |
1 / 22
Acknowledgements
Funding:
- I receive an RTP Scholarship from the Australian Government and a Scholarship from NDARC
- NDARC receives funding from the Australian Government Department of Health
Thanks to my PhD Supervisors: Tim Dobbins, Richard Mattick and Raimondo Bruno.
2 / 22
Overview
- Background;
- Bias in causal inference;
- Assumptions in causal inference;
- Methods for causal inference;
- Targeted maximum likelihood estimation;
- TMLE Examples;
- Conclusions;
- References;
3 / 22
Background
- Causal inference at its simplest:
- "the difference in a given outcome, based on some prior event, compared with what would have happened had that event not occurred"
- RCTs are, and will remain, the gold standard
- There are times when RCTs aren't possible
- Causal inference is possible without randomization
- It just requires more caution
4 / 22
Bias in causal inference
- General to all observational studies
- Selection bias
- Confounding
- Collider bias
- Measurement error
- Specific to longitudinal analysis
- Loss to follow-up
- Exposure affected time-varying confounding
5 / 22
Bias in causal inference
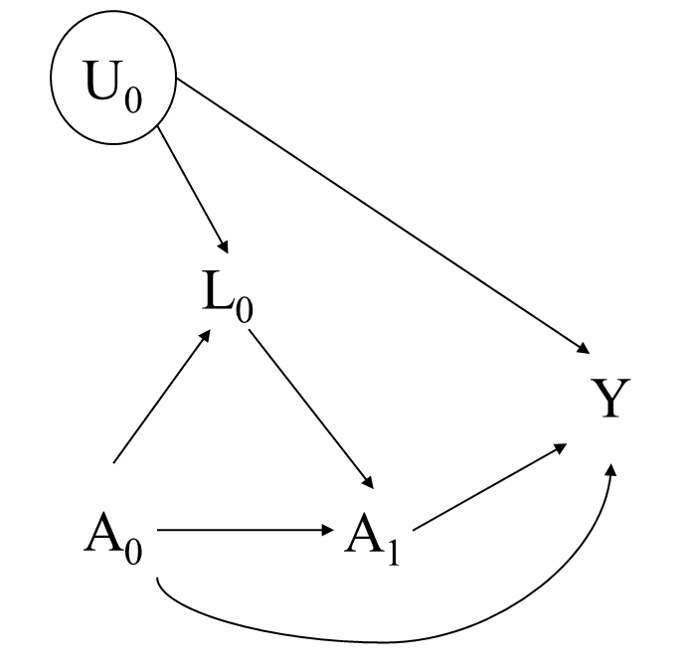
6 / 22
Bias in causal inference
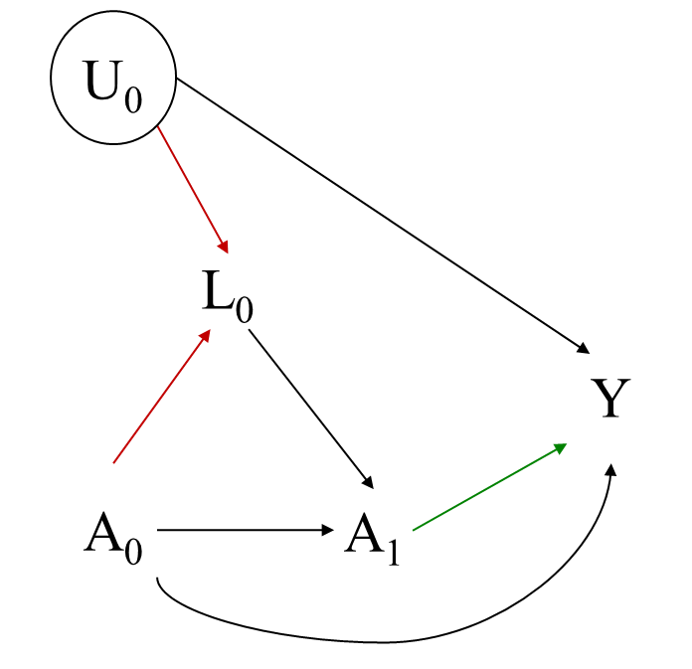
7 / 22
Bias in causal inference
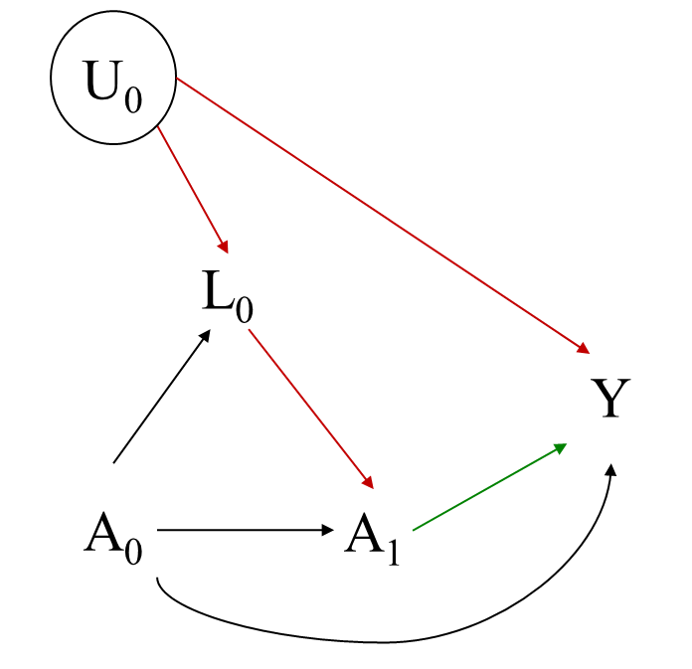
8 / 22
Assumptions in causal inference
- No interference
- Consistency
- Positivity
- No unmeasured confounding
9 / 22
Methods for causal inference
- Propensity score matching (PSM)
- Marginal Structural models (MSM)
- G-computation
- Doubly-robust methods (DR)
10 / 22
Methods for causal inference
- Doubly-robust methods (DR)
- At their simplest: DR methods are those that provide consistent estimates even when one of either the propensity or outcome models are estimated consistently 'Simple' DR methods:
- adjusted IPTW
- IPTW weighted
- G-computation
- A-IPTW
- Similar to IPTW, but adjusts the IPTW estimate by a function of the outcome model
- There is some discussion about the best approach for this in terms of estimating the models
11 / 22
Targeted maximum likelihood estimation
- TMLE is a targeted substitution estimator that treats everything except the target estimand as 'nuisance' parameters
- TMLE involves:
- estimating an initial conditional expectation of an outcome using maximum likelihood,
- estimating the propensity score,
- using the propensity score to create a 'clever' covariate h, and
- updating the outcome model based on a function of the initial estimates and the clever covariate
12 / 22
Targeted maximum likelihood estimation
- This can be repeated if necessary, and will iterate to the target parameter
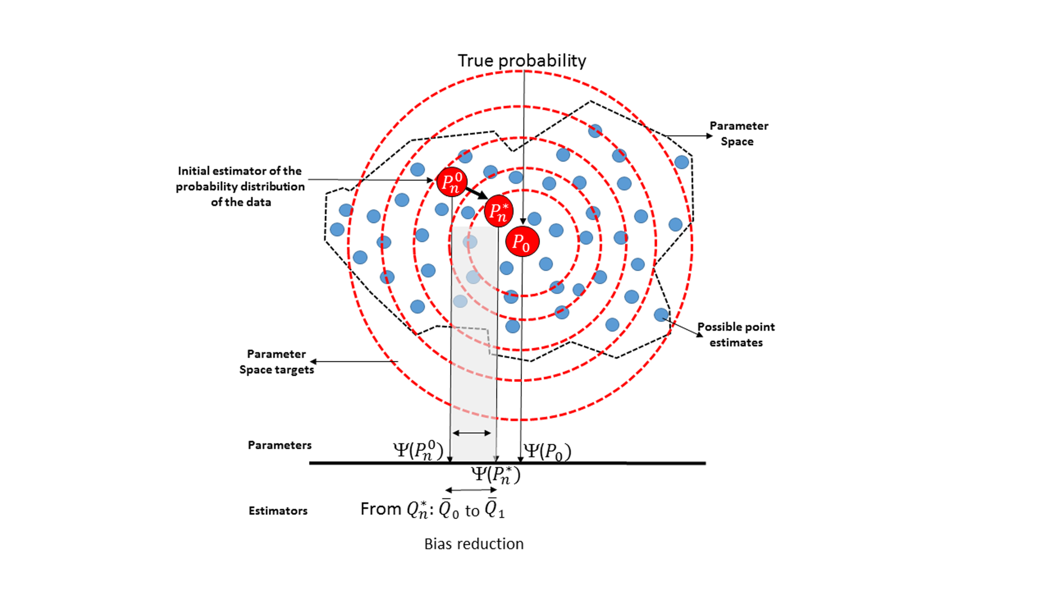
- However, it has been shown that most common effect measures can be estimated in one iteration
13 / 22
Targeted maximum likelihood estimation
- Because it is a substitution estimator that doesn't use the parameters of the initial models, TMLE is commonly estimated using ensemble machine learning
- The ensemble machine learning algorithm 'Super Learner' was developed in parallel with TMLE
- The packages 'tmle' and 'ltmle' in R both call 'SuperLearner' by default
14 / 22
Targeted maximum likelihood estimation
- TMLE is relatively new
- There are a number of areas of ongoing investigation regarding the performance:
- Balance SuperLearner: an adaptation of the SL algorithm optimized for balance rather than accuracy of prediction
- Collaborative TMLE, which uses a loss function based on Q to fluctuate the nuisance parameter, instead of a loss function of the nuisance parameter itself. C-TMLE can be a consistent estimator even when both models are misspecified
15 / 22
TMLE Examples
- Random data following the DAG from earlier
- True parameter is:
Joint = 0.5ÃA_0 + 1.5ÃA_1 - 1.0ÃA_0ÃA_1 = 1.0

16 / 22
TMLE Examples
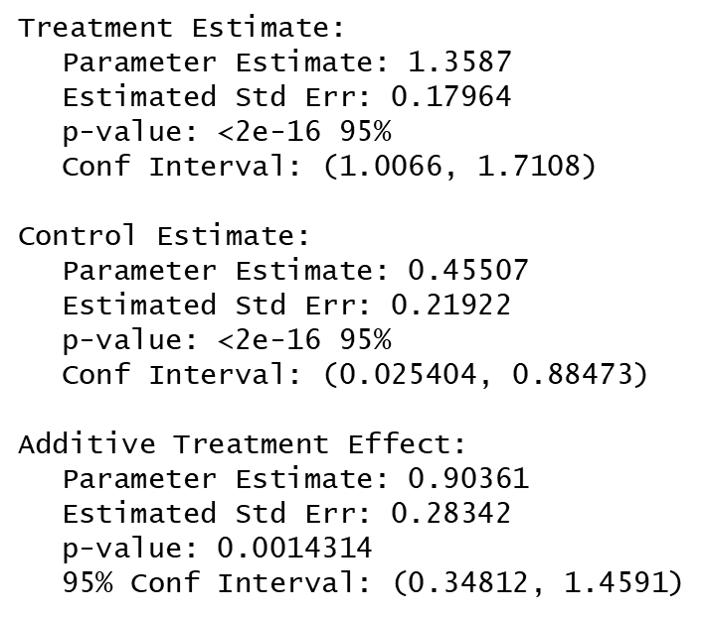
17 / 22
TMLE Examples
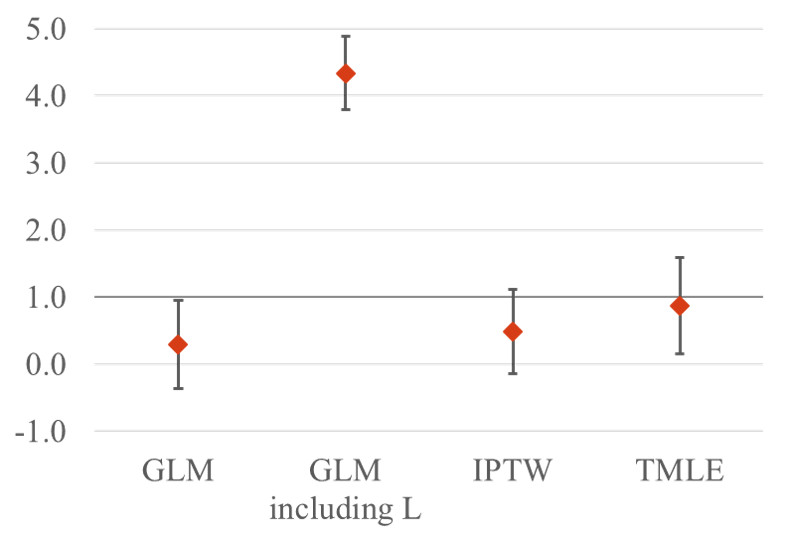
18 / 22
TMLE Examples
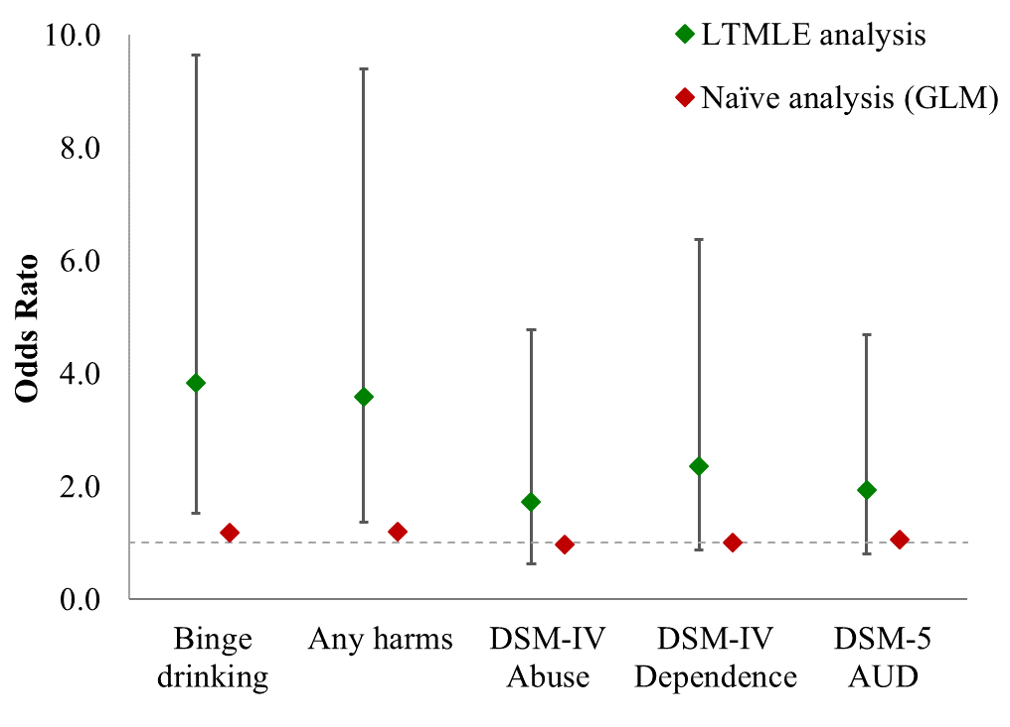
19 / 22
TMLE Examples
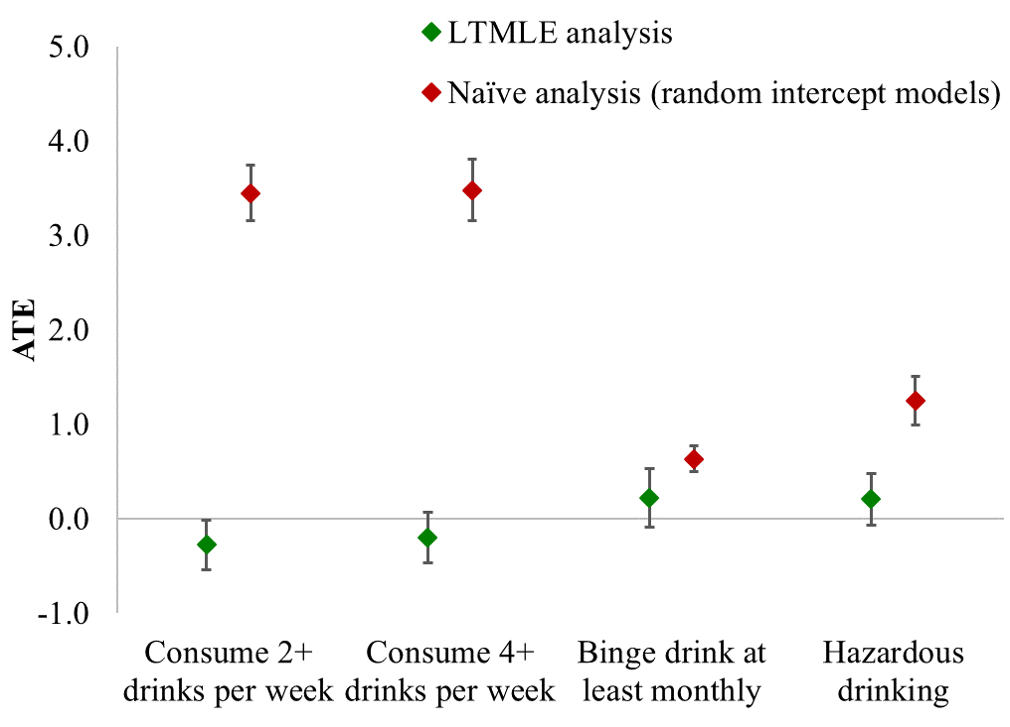
20 / 22
Conclusions
- Unbiased causal inference is possible in non-randomized studies
- There are methods to deal with bias
- Newer methods are more robust
- Even for analysis of association, bias is an issue that can be addressed by these methods
- Markdown for a TMLE tutorial currently under review at Statistics in medicine: https://github.philipclare.com/tmletutorial
21 / 22
References
- Clare PJ, Dobbins TA, Mattick RP. Causal models adjusting for time-varying confounding-a systematic review of the literature. Int J Epi. 2019;48(1):254-265.
- Robins JM. Marginal Structural Models. 1997 Proceedings of the American Statistical Association, Section on Bayesian Statistical Science. 1998:1-10.
- Robins JM. A new approach to causal inference in mortality studies with a sustained exposure period-application to control of the healthy worker survivor effect. Mathematical Modelling. 1986;7(9):1393-512.
- Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61(4):962-72.
- Van der Laan MJ, Rubin D. Targeted Maximum Likelihood Learning. Int J Biostat. 2006;2(1).
22 / 22